Making Sense of Exponential Models

Exponential growth is a topic that deserves especially thoughtful treatment as part of a high school education because a person who has thought deeply about this ubiquitous phenomenon pays attention to and conceptualizes certain critical issues in, for example, science, economics, and social science, in a fundamentally different way than one who is oblivious to or overwhelmed by the concept. (For one of the more extreme examples of the importance of being in the habit of thinking about growth models, see Section e—pun entirely coincidental, I’m sure—on page 2 of a bill passed by the North Carolina House of Representatives in April 2012, which got lots of attention after it was featured on the Colbert Report.)

In addition, exponential growth is a topic in the precalculus curriculum where I’ve found that intertwining aspects of “pure” and “applied” math is an unusually effective tool for deepening student understanding of some key mathematical ideas and for helping students to develop a sense of the power of abstraction. It is one of the high-school-level “pure math” ideas that most students have already encountered repeatedly—usually without really recognizing it—in their daily lives (while reading a Buzzfeed aritcle, for example) and where they already have the necessary mathematical and life experience to make sense of many contexts in which the concept is relevant.

Unfortunately, most textbooks present applications of exponential growth in a way that fragments consideration of problem “types” to such an extent that it is virtually impossible for students to have any sense of the forest because the focus is so intensely on pointing out relatively minor features of individual trees. The result of following such texts closely is that—in this area where it is so important for students to understand the central concept and be able to use it flexibly in the myriad of ways they will encounter it—students resort to memorizing a dozen different formulas and looking for similarities in the surface features of problems to figure out which of these formulas to use. With this approach, students have their conceptions of math as a “cookbook” discipline requiring memorization of meaningless details reinforced, and are inadvertently encouraged to think about radioactive decay as a fundamentally different problem than, say, continuous compounding of interest, annual growth in a population, or doubling time of an investment.

Back in the day when I followed the textbook’s lead on this topic, I invariably ended up frustrated by both the slog through it and the results. I was helped in my quest to come up with a better way by reading what Daniel Willingham has written about how our brains are wired to see surface structure, but that as we invest lots of time and thought in an area we become experts, distinguished from novices by the propensity to classify problems and ideas on the basis of their deep structure rather than than their surface structure. As I’ve worked to refine my understanding of the deep structure underlying exponential growth applications and have sought to develop approaches and emphases more geared toward helping students see this deep structure I have traveled from a place where exponential modeling was probably the worst part of my precalculus courses to a point where it’s both one of the best and, not coincidentally, deeply integrated with major themes of the course.

Here is a set of questions I have found useful to pose to my precalculus students early in our consideration of exponential functions:

1. Graph the following pairs of equations. You should see a clear relationship between the graphs in each pair. Try to articulate an algebraic explanation for the relationships you observe:
   1. $$f_1(x)=2^{x+3}$$ and $$g_1(x)=8\cdot 2^x$$
   2. $$f_2(x)=3^{x+2}$$ and $$g_2(x)=9\cdot 3^x$$
   3. $$f_3(x)=4^{x-1}$$ and $$g_3(x)=\frac{1}{4}\cdot 4^x$$
2. Give two different equations, similar to the pairs in #1, for this graph:
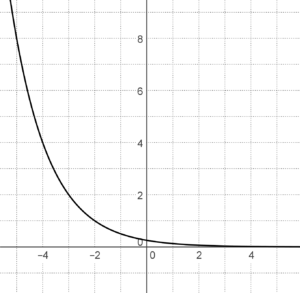
3. Is it possible to think of the function $$g(x)=8^x$$ as a transformation of the function $$f(x)=2^x$$? If so, describe the transformation as precisely as you can. If not, explain why not. How would your answer change if $$g(x)=9^x$$?

The focus that these questions put on thinking about multiple ways of writing the same exponential functions builds an important foundation for the consideration of applications of exponential functions. Ultimately, I want students to develop a deeply-rooted understanding that exponential growth represents a fundamentally different and much bigger change over time than linear change and I hope that if they ever need to develop a mathematical model for a situation involving exponential growth, they will first think $$f(x)=a\cdot b^x$$ and then ask themselves, “In what form would I like to write this exponential relationship so that it is easiest to work with or so that my choice of form emphasizes what I am most interested in emphasizing about the relationship here?”

Questions like #2 above—when included as part of an approach emphasizing function transformations and the powerful concept of “negative” in all different contexts—help students to think of exponential decay from almost the time of their first formal introduction to it as mathematically exactly the same as exponential growth. When a student gets this, there is no need for the two separate boxed formulas you are likely to find in textbooks labeled “Exponential Growth Model” and “Radioactive Decay Model”, and differing only by a negative sign. (The decay model probably includes an additional formula telling you that you need to remember that r in this case is equal to ln 2 divided by the half-life.) I discovered through hard experience, probably first as a student, but much more consciously as a teacher that this kind of boxed formula gives students the mistaken impression that if you’ve got radioactive decay, this is the only formula you can use and nothing else you might know about exponential functions is relevant. I don’t think it’s an overstatement to say that this is a big impediment to truly understanding exponential growth and that in the interest of trying to make it easier for students to figure out how to get the answers to problems in the textbook the authors make it less likely that people will develop the type of understanding that will actually be useful to them in conceptualizing the real universe, the mathematical universe, and the intimate connections between them.

The last part of Question #3 above is what really sets the stage for understanding the various ways in which we might choose to model exponential growth in a particular context. Students typically answer that $$g(x)=8^x$$ can be thought as transformation of the function $$f(x)=2^x$$ (even if they’re unsure of exactly how), but they almost invariably say that $$g(x)=9^x$$ cannot be. Here’s a quick Desmos sketch that helps them see that $$g(x)=9^x$$ can be written as $$f(x)=2^{px}$$ and begs the question of  what the exact value of p is. The answer provides nice reinforcement of the definition of inverse functions, though it takes assigning one problem per day like this over multiple days (and occasionally, forever after) to make most students really comfortable with the algebra of the problem.

Here’s a nice early attempt at a solution to the question “Write the function $$f(x)=3^x$$ as an exponential function with a base of 2.”

Having taken a graphical exploration approach to the problem, this student (who had an “Aaaaa . . . why didn’t I think of that?!?” reaction) learned very quickly to appreciate and use the solution method offered by a classmate:

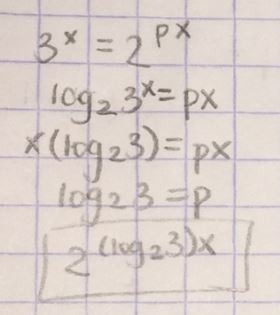
Once this algebraic approach–supported by the visual understanding–has sunk in, however, students have a good foothold for recognizing the common deep structure among various ways of modeling exponential growth.

The one other thing I make sure we’ve done well in advance of our consideration of compounding interest multiple times in a year is the following exploration. (In actuality, I present question E1 on the board since it’s such a great discussion generator. It typically leads us into an unprompted consideration of E2. I then have students work through the remaining questions on their own or in small groups.)

I follow this up by regularly including homework or class warmup questions like “Find both a decimal approximation to the nearest thousandth and the exact value of $$\displaystyle\lim_{x\to\infty}\left(1+\frac{0.5}{x}\right)^x$$.” When students are already used to seeing this limit as a power of e, the leap from discrete compounding periods to continuous compounding becomes much easier and the impact of seeing the connection is much greater.

With this background in place, I then move on to a consideration of exponential growth in a variety of contexts. Ultimately, I want students to be aware of three particularly useful forms of exponential equations in addition to the basic $$f(x)=a\cdot b^x$$, to be able to transform equations from any one of these to any other, and to understand that the actual percentage change per unit of time in which t is measured is represented explicitly by  r in the first of these.

1. $$A(t)=A_o(1+r)^t$$
2. $$A(t)=A_oe^{rt}$$
3. $$A(t)=A_o\cdot c^{t/d}$$

The key things I want students to be in the habit of keeping in mind about each form are

1. Here r is the percentage change per unit of time. The 1 keeps our initial amount, the r tells us what portion of the amount present at the beginning of the time period is added (if r is positive) or taken away (if r is negative) each time period. There’s really no difference between this and $$f(x)=a\cdot b^x$$ except that we’re explicitly thinking about the base as $$1+r$$.
2. Here r is the continuous or relative rate, which is smaller than the value of r we’ll get when we convert to Form 1 because of the effect of compounding.
3. Here d is how long it takes for the amount to change by a factor of c. Assuming that d is positive, a value of c smaller than 1 represents decay rather than growth.

I do also want students to be able to use the form $$A=A_o\left(1+\frac{r}{n}\right)^{nt}$$, but we don’t include it in our summary of three main forms since—as far as I know—it is really only used in banking. It is quite important from a mathematical perspective, however, because it serves as the bridge between Form 1 and Form 2 and as such provides a helpful concrete illustration of the limiting process. When we get to the summary stage, we usually write it off to the side with an arrow pointing to the space between Forms 1 and 2.

We also talk about the fact that in a banking context, the r in each form is the APR and that in the first form this is the same as the APY. I have found that encouraging students to think about what APY would mean in, say, a population problem helps them remember the distinction between the Form 1 r and the Form 2 r.

Resources

• Sections 3.1 and 3.2 of the precalculus book that my colleague Travis Ortogero and I have been developing provides a sense of the general path I follow as we consider applications of exponential functions.
• I use problems like the following to reinforce the idea that you can always convert from one form of an exponential equation to another:

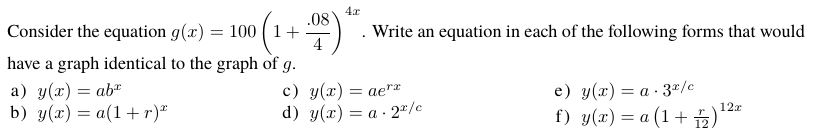
• Here is a set of problems that can be used to help students recognize that you can choose which form you want to use based on what information you’re given.
• This Desmos Activity is intended to help students deepen their understanding of the meaning of parameters in equations modeling exponential growth and to provide practice converting among various exponential forms. Students are given an equation modeling the population of North Carolina as a function of time at the outset. While a graph of the actual population data is shown in the course of the activity, the focus is not on going from data to a model, but on thinking about how the same model can be written in a variety of forms.
• I also developed this set of cards which I’ve found to be particularly good at getting students to wrestle with the significance of the parameters in the various exponential equation forms. Given the knowledge that the a cards can be paired with the f(x) cards in such a way that all of the functions will be the same when the matches have been properly made, students can do all of the matching using logic and knowledge of the forms alone. They can also determine which f card goes with each of the two blank a cards, and figure out these a values, to the specified number of significant figures. And–gotta love Desmos–here is the Desmos Card Sort version! (Even if you decide to use the paper version, the Desmos version will be great for going over the activity as a class.)