Quadratic Functions with Desmos Activity Builder

I thoroughly enjoyed using an activity I created using Desmos Activity Builder over the course of the past couple of days with my precalculus students to help them think in new ways about quadratic functions. These are intelligent people who have graphed plenty of parabolas and solved plenty of quadratic equations in Algebra 1 and 2, and have worked extensively this year with transformations of functions in general and transformations of power functions, exponential functions, and log functions in particular. A couple of months ago, they were successfully answering questions on tests asking them to find equations of power functions like these:

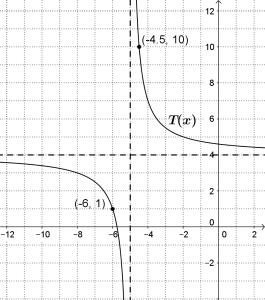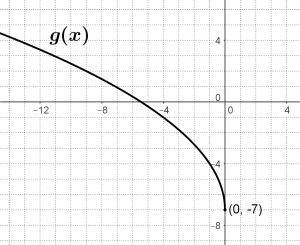In the Desmos activity, the task was to enter an equation of a parabola that would go through a set of three points. If you’d like to try the activity yourself before reading on, you can do so here.

In the first few cases, one of the points was the vertex, and in most of the others two of the points had the same y-coordinate. Students had a few minutes to start the activity in class on Thursday, and were asked to continue working through it for homework. I told them they should feel free to stop working after 30 minutes, as long as they included thoughtful answers on the first two screens which required some writing.

If you think this would be a piece of cake for precalculus students with the background I’ve described, you would have been interested to hear the chorus of “That homework was so hard!” as students arrived to class on Friday. Knowing how to graph a parabola, or solve a quadratic equation, or even understanding what effect all of the parameters in a quadratic equation in vertex form have on the the graph of the equation does not make it immediately obvious how to write an equation given three points, even when those points are specially chosen to eliminate the need to write three equations in three unknowns. The fact that students can use a guess-and-check approach, however, means that everyone has a way of making progress.

All students did produce graphs that went through (or very, very, close to through) the points in first three cases (the ones where the vertex was given). We had an enjoyable time as a class looking through the solutions to third case and comparing the ways in which students wrote the equation, wondering what that might imply about different ways in which people went about finding the equation, and figuring out which were exact and which were approximate.

$$f\left(x\right)=0.285714\left(x-1\right)^2-5$$ $$f\left(x\right)=.285\left(x-1\right)^2-5$$ $$f\left(x\right)=\frac{2}{7}\left(x-1\right)^2\ -5$$ $$f\left(x\right)=\frac{\left(x-1\right)^2}{3.5}-5$$ $$f\left(x\right)=-5+1.14\left(\frac{x-1}{2}\right)^2$$ $$f\left(x\right)=\frac{14}{49}\left(x-1\right)^2-5$$

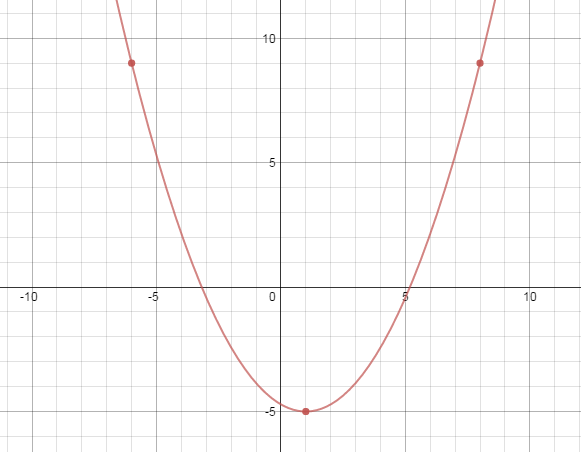We then looked at what students had written in response to the question, “Write down any questions you have about the first three screens and/or provide a summary of how to solve such problems.”

While students were able to find the horizontal and vertical shift pieces of the equations without guess and check, they relied heavily on guess and check for determining the stretch factor, though clearly a few had consistently been able to figure out the stretch factor by thinking carefully about the transformation of the $$y=x^2$$ graph. The comments indicate a strong interest in  finding an alternative to guess and check, and careful reading of the answer at the bottom of the left column provided the answer students were looking for. Following the directions provided there made it obvious where the student who had $$\frac{14}{49}$$ as the quadratic term coefficient had gotten that. There was lots of, “Oh! Why didn’t I think of using an a!?!” and “It would have been so much easier if I had thought of that!” A little appreciation for the power of algebra. Some admiration for the one student who had developed and described an efficient combination of geometric and algebraic approaches.

In the next set of screens, despite the fact that it was the x-intercepts and not the vertex that were given, all but two students continued to write their equations in the form which showed the vertex explicitly. As we clicked through student responses to the first of these and eventually landed on the screen of a student who had written the equation in the form $$f\left(x\right)=\left(x+1\right)\left(x-5\right)$$, a few students immediately let out a cry of recognition that someone had discovered an easier approach.

When we got to the screen showing the thumbnail view of everyone’s graphs for the second of the intercept cases,  people were immediately intrigued by one graph that was not a parabola. After we admired it briefly, and talked about why it didn’t meet the definition of a quadratic function, someone realized that we could turn the graph into a parabola if we just changed the exponent on $$\left(x-5\right)$$ from a 3 to a 1. People began to recall having looked at graphs of polynomials in Algebra 2 and some connections about a quadratic being a pretty simple polynomial were made.

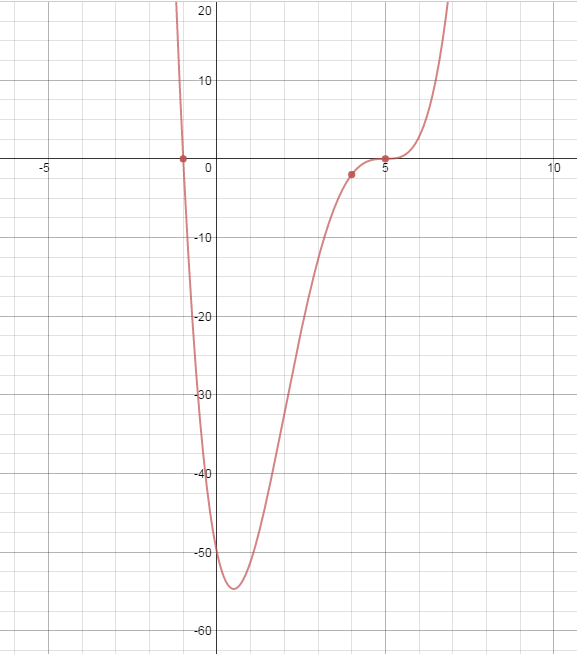$$f\left(x\right)=.4\left(x+1\right)\left(x-5\right)^3$$

No one had completely solved the case where there were sliders for m and n, and the three points were $$\left(m,0\right)$$, $$\left(n,0\right)$$, and $$\left(0,7\right)$$, but one student had gotten as far as the $$f\left(x\right)=\left(x+m\right)\left(x-n\right)$$. Before long, someone realized we could use the power of algebra we had recalled earlier in the period and, after introducing an a, we soon had an expression for the “stretch factor” in terms of m and n. The excitement in the room once we added that coefficient and started moving the sliders was impressive. “That is so cool!” “Can you go more slowly through that place where it turns upside down?” “What happens right there where it turns upside down?” “Why is that m can’t be 0?”

While doing the homework, only one person proceeded to the cases where the symmetric points were not on the x-axis, but when the class looked at the equation she had written to solve the first of these, many saw right away that she had solved it by thinking of it as a vertical shift of the intercept form. I’m hopeful that having come to this insight this way will help students to see and more easily remember how they can go from the standard form of a quadratic equation to its graph without having to complete the square and without relying on having memorized that the x-coordinate of the vertex is $$-\frac{b}{2a}$$ (and students who think about this form of a quadratic equation carefully, can finally see why $$-\frac{b}{2a}$$ must be the x-coordinate of the vertex.)

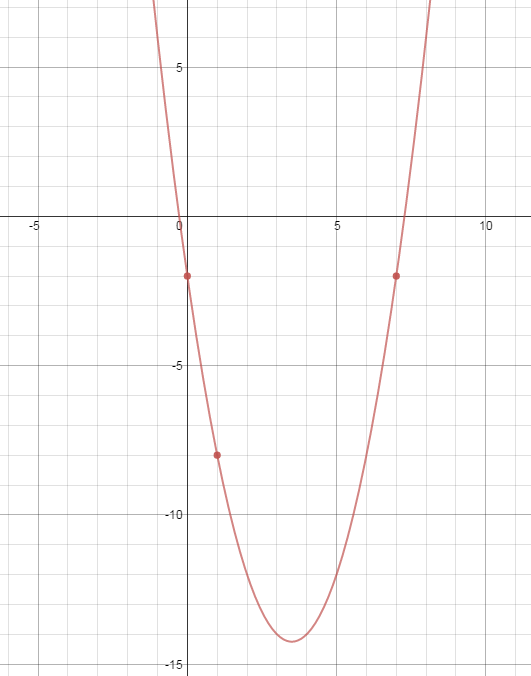$$f\left(x\right)=x\left(x-7\right)-2$$

I look forward to seeing how students do with the general “shifted-intercept form” case (where the points are $$\left(0,n\right)$$, $$\left(m,n\right)$$, and $$\left(1,-3\right)$$) this weekend and to seeing what progress they make with the final case where they are given the y-intercept and two other points.

Thanks, Desmos folks for developing such a truly fabulous tool! I love how intuitive Desmos is, how nice the graphs and equations look, how it provides an alternative way of considering familiar concepts, and how easy it is to create something like this in the Activity Builder. In closing, here is my current wish list for things that would make the Activity Builder even more awesome:

• an option to hide (or at least lock) folders in student view
• an option to hide student names in the teacher view
• an option to hide student names when allowing students to see other students’ responses to a particular question
• the ability to select a subset of student responses on a single question and an order for clicking through them
• the ability to use LaTex when writing notes and/or titles
• an option for the teacher to save student responses at a particular point in time
• an option to send a comment to a student as they’re working