A Modern Log Table

After re-reading the first chapter 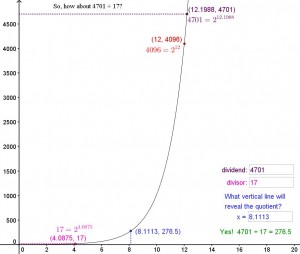of Eli Maor’s e: The Story of a Number, I ended up spending a couple of days creating a GeoGebra applet which I’ve called Napier’s Gift. Given that it’s July, I didn’t have a class to try it out on, so I convinced my daughter (who will be going into 8th grade in the fall) to alpha-test it for me. She’s not usually interested in my math obsessions, so I was very grateful to her for agreeing to serve as a guinea pig. The current version is definitely better for her input. She’s had beginning algebra and had worked with division of numbers written with like bases already, but had never seen logs. She didn’t read the Napier quote that appears at the top of the applet before beginning, but when I asked her at the end to read it and summarize what she thought it meant, she said “There’s a hard way and a shortcut. The hard way is to divide the actual numbers . . . and the shortcut is to subtract the exponents.” Yes. She got it. After she’d finished the applet, I pointed to one of the ordered pairs on a graph in the applet and said that in higher math the coordinate that’s the exponent is called the logarithm of the other number. She asked, “Couldn’t that number have other logarithms depending on its base?” Yes. She got it. I mentioned that logarithms tend to be difficult for high school students when they first see them. She asked which students and I said, “Almost all of them.” She replied, “Really? I feel like I could have figured it out because the logarithms and the exponents are like opposites.” Yes. She got it.

(If you experience any problems with the link to the applet above, you can try viewing it on GeoGebraTube instead.)